By Evalf, and other Nutils contributors

officialfinite strainenergy minimization

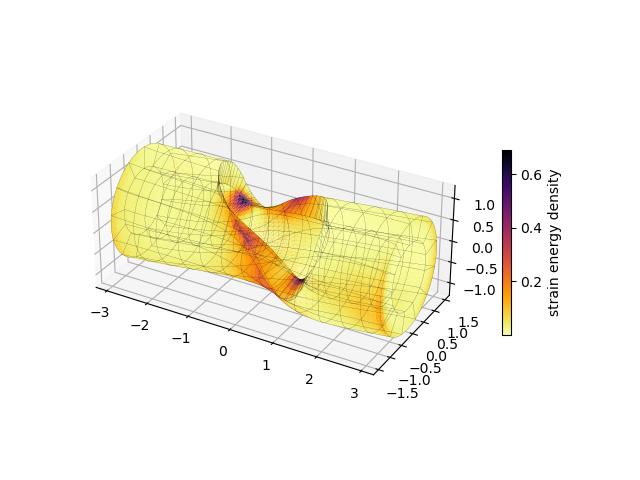
This script simulates the deformation under torque of a hollow cylinder with a circular cutout in its wall. The cylinder is modeled as a Neo-Hookean solid that is clamped on both ends while being twisted at fixed angular increments.

Dimensions are normalized to the radius of the cylinder, measured at half the thickness of the material. Since the problem is entirely kinematic, stiffness does not affect the resulting shape (it merely scales the energy) which leaves compressibility as the only relevant material parameter. We therefore define the strain energy density function simply as

W = F : F - 3 - 2 log(|F|) + D (|F| - 1)^2

Here F is the deformation gradient with respect to the reference geometry, and D is defined as ν / (.5-ν), using Poisson's ratio ν consistent with linear theory. The equilibrium state follows from minimizing the integrated energy subject to constraints.

More information on Neo-Hookean and other hyperelastic materials can be found at https://en.wikipedia.org/wiki/Hyperelastic_material.