By Evalf, and other Nutils contributors

officialNavier-StokesRaviard-Thomascompatible spaces

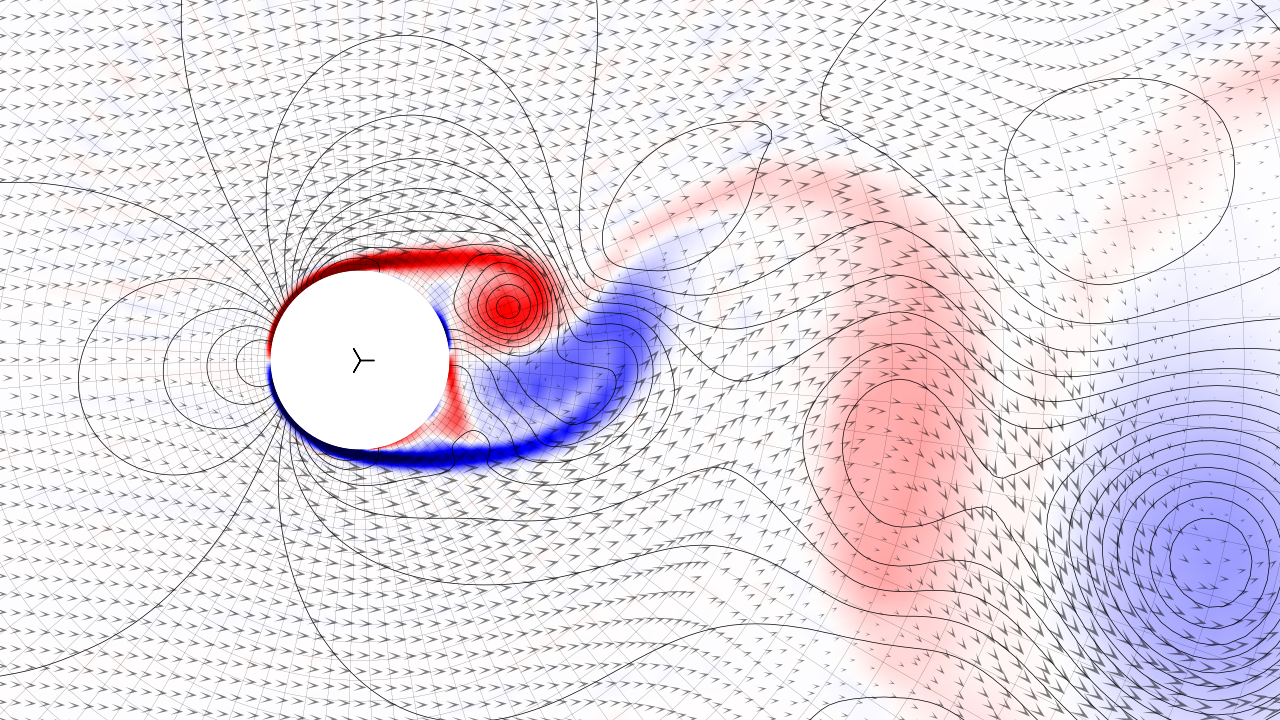
Solves the Navier-Stokes equations around a cylinder, demonstrating different flow regimes at different Reynolds numbers.

The general conservation laws are:

Dρ/Dt = 0 (mass)
ρ Du_i/Dt = ∇_j(σ_ij) (momentum)

where we used the material derivative D·/Dt := ∂·/∂t + ∇_j(· u_j). The stress tensor is σ_ij := μ (∇_j(u_i) + ∇_i(u_j) - 2 ∇_k(u_k) δ_ij / δ_nn) - p δ_ij, with pressure p and dynamic viscosity μ, and ρ is the density.

Assuming incompressible flow, we take density to be constant. Further introducing a reference length L and reference velocity U, we make the equations dimensionless by taking spatial coordinates relative to L, velocity relative to U, time relative to L / U, and pressure relative to ρ U^2. This reduces the conservation laws to:

∇_k(u_k) = 0 (mass)
Du_i/Dt = ∇_j(σ_ij) (momentum)

where the material derivative simplifies to D·/Dt := ∂·/∂t + ∇_j(·) u_j, and the stress tensor becomes σ_ij := (∇_j(u_i) + ∇_i(u_j)) / Re - p δ_ij, with Reynolds number Re = ρ U L / μ.

The weak form is obtained by multiplication of a test function and partial integration of the right hand side of the momentum balance.

∀ q: ∫_Ω q ∇_k(u_k) = 0 (mass)
∀ v: ∫_Ω (v_i Du_i/Dt + ∇_j(v_i) σ_ij) = ∫_Γ v_i σ_ij n_j (momentum)

The exterior boundary is strongly constrained to uniform inflow in the upstream section, and traction-free in the downstream section, in both cases eliminating the right hand boundary integral. The no-slip condition at the interior boundary is constrained strongly in the normal component, and weakly in the tangential component using Nitsche's method. The added boundary integral is scaled to dominate the right hand side of the momentum balance.

For the initial condition we take potential flow, meaning the velocity equals the gradient of a harmonic potential field. In order to obtain coefficients against the required basis the flow problem is solved as a coupled first order system: ∇_k(u_k) = 0 and u_i = uinf_i - ∇_i(p), where the free flow velocity uinf is introduced so that the scalar field p is zero at infinity. The weak formulation takes the form of an optimization problem:

∂/∂(u,p) ∫_Ω (.5 Σ_i (u_i - uinf_i)^2 - ∇_i(u_i) p) = 0

The script uses a Raviart-Thomas discretization in curvilinear coordinates, resulting in a pointwise divergence-free velocity field. The polar mesh is constructed such that all elements are geometrically similar, growing exponentially with radius and placing the artificial exterior boundary at large (configurable) distance. The reference length is set equal to the diameter of the cylinder and the referency velocity to the magnitude of the inflow velocity, meaning that both quantities are simulated at unit value.