By Evalf, and other Nutils contributors
officialelectro-magnetism
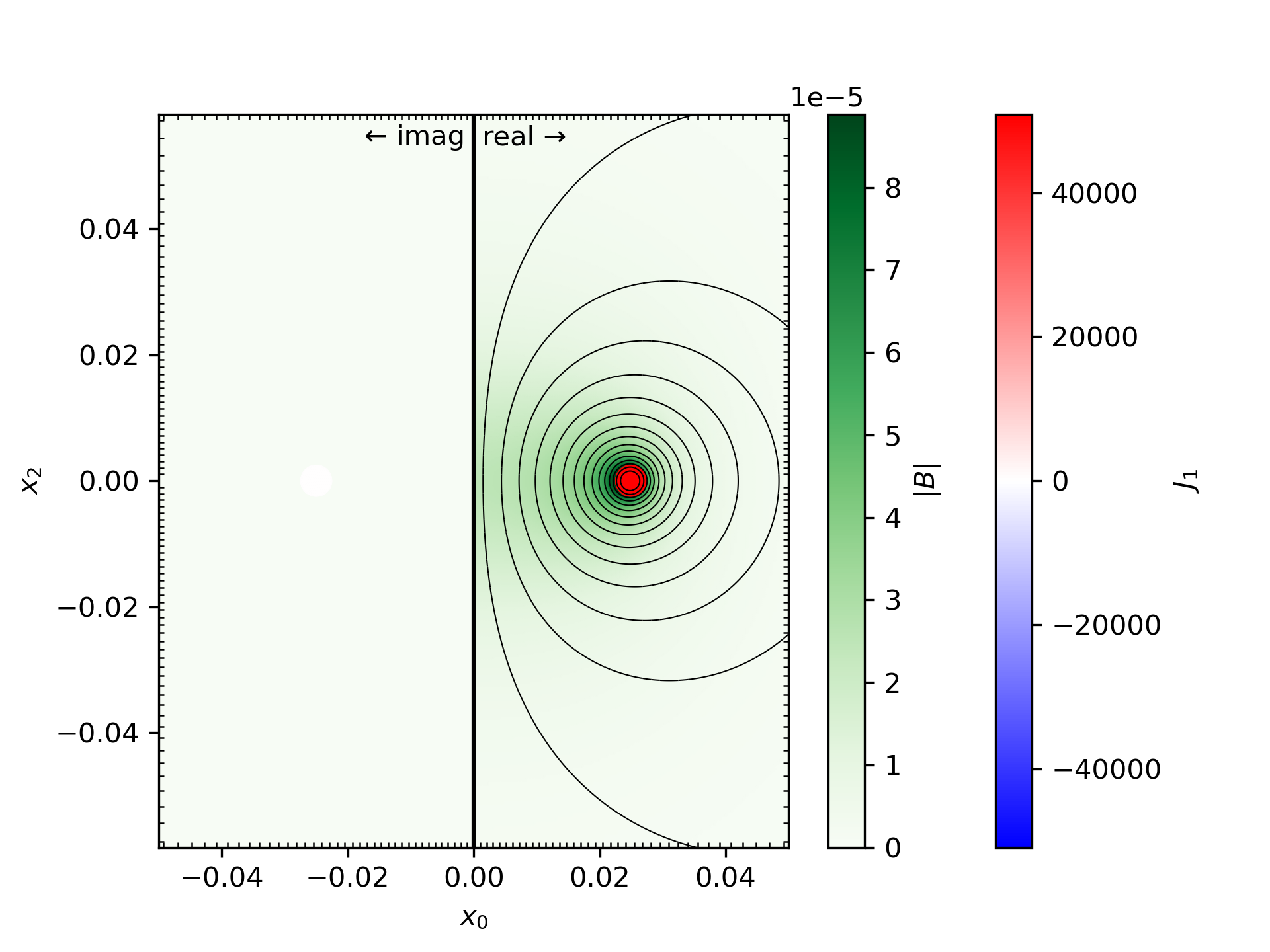
Computes the magnetic field induced by a DC or AC current in one or several toroidal conductors. This problem is modeled with the quasi-static magnetic vector potential with Lorenz gauge:
∇_j(∇_j(A_i)) = -μ0 J_i
where A is the magnetic vector potential, J the current density and μ0
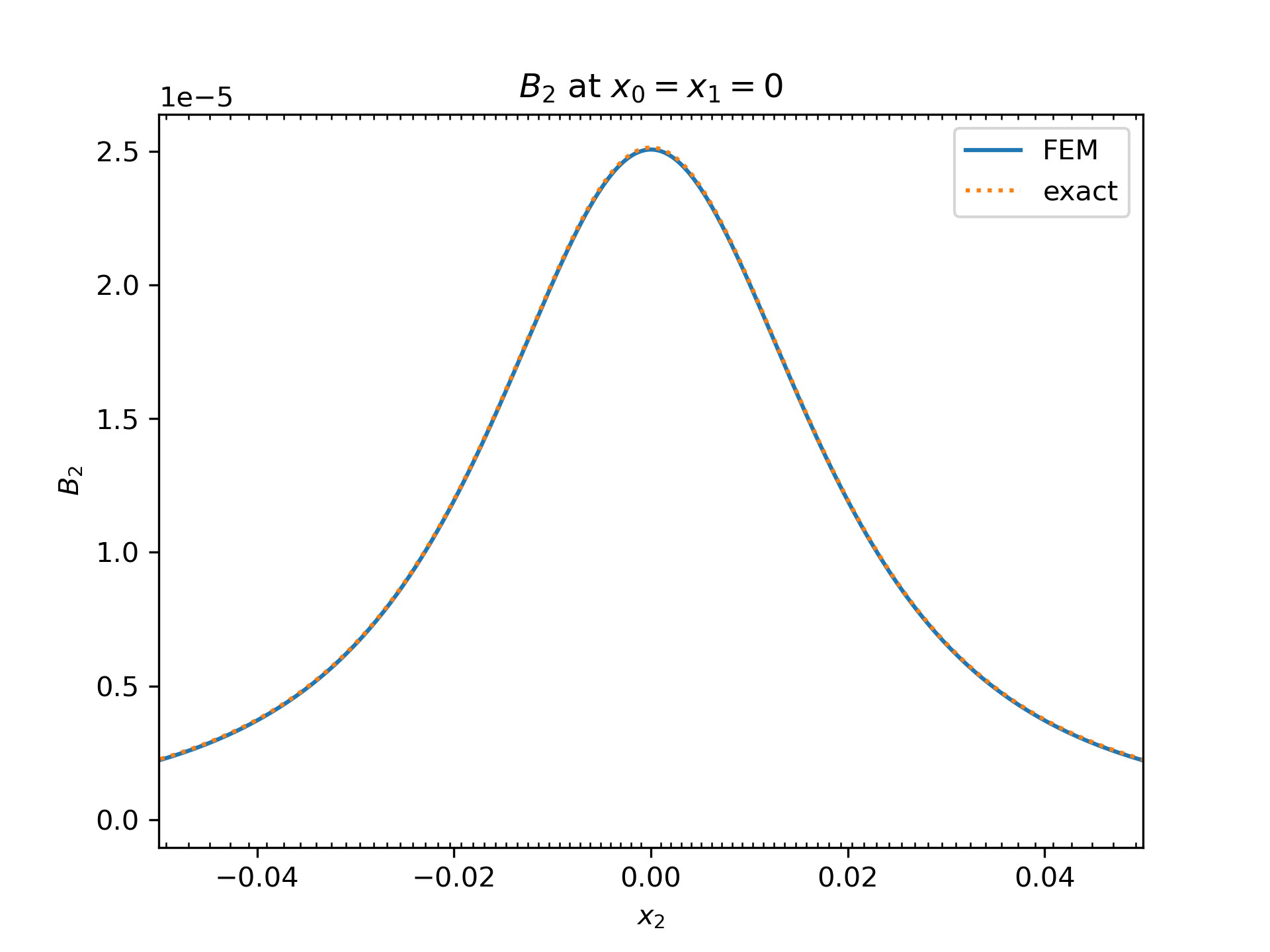
the magnetic permeability. The magnetic field B is then given by the curl
of the magnetic vector potential. The current density is the sum of an
external current Jext and the current induced by the magnetic field,
Jind. The external current is given by
Jext_i = (I / π rwire²) cos(ω t) eθ_i
inside the conductor and zero everywhere else, where ω = 2 π f. The induced
current follows from Faraday's law of induction and Ohm's law:
Jind_i = -σ ∂_t(A_i)
where σ is the conductivity, which is non-zero only inside the conductor.
We can solve the temporal component of A by letting A_i = Re(Â_i exp(j ω t)). This problem in terms of  is:
∇_j(∇_j(Â_i) = -μ0 Ĵ_i
with
Ĵext_i = (I / π rwire²) eθ_i
and
Ĵind_i = -j ω σ Â_i