By Evalf, and other Nutils contributors

officialCahn-Hilliard

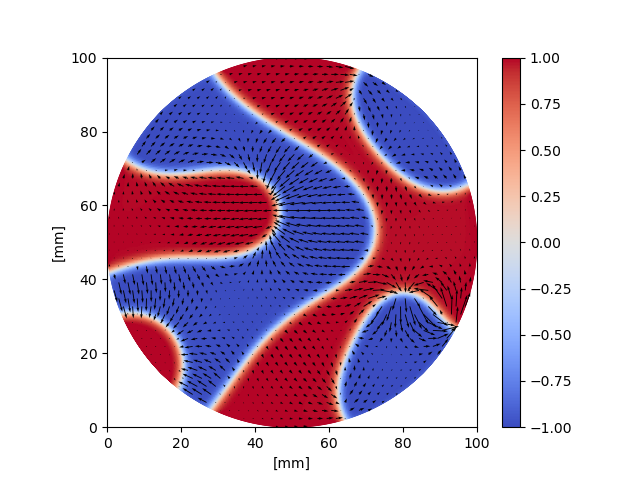
Solves the Cahn-Hilliard equation, which models the unmixing of two phases (φ=+1 and φ=-1) under the influence of surface tension. It is a mixed equation of two scalar equations for phase φ and chemical potential η:

dφ/dt = -div(J(η))
η = ψ'(φ) σ / ε - σ ε Δ(φ)

along with constitutive relations for the flux vector J = -M ∇η and the double well potential ψ = .25 (φ² - 1)², and subject to boundary conditions ∂ₙφ = -σd / σ ε and ∂ₙη = 0. Parameters are the interface thickness ε, fluid surface tension σ, differential wall surface tension σd, and mobility M.

Cahn-Hilliard is a diffuse interface model, which means that phases do not separate sharply, but instead form a transition zone between the phases. The transition zone has a thickness proportional to ε, as is readily confirmed in one dimension, where a steady state solution on an infinite domain is formed by η(x) = 0, φ(x) = tanh(x / √2 ε).

The main driver of the unmixing process is the double well potential ψ that is proportional to the mixing energy, taking its minima at the pure phases φ=+1 and φ=-1. The interface between the phases adds an energy contribution proportional to its length. At the wall we have a phase-dependent fluid-solid energy. Over time, the system minimizes the total energy:

E(φ) := ∫_Ω ψ(φ) σ / ε + ∫_Ω .5 σ ε ‖∇φ‖² + ∫_Γ (σm + φ σd)
        \                \                  \
         mixing energy    interface energy   wall energy

Proof: the time derivative of E followed by substitution of the strong form and boundary conditions yields dE/dt = ∫_Ω η dφ/dt = -∫_Ω M ‖∇η‖² ≤ 0. □

Switching to discrete time we set dφ/dt = (φ - φ0) / dt and add a stabilizing perturbation term δψ(φ, φ0) to the double well potential for reasons outlined below. This yields the following time discrete system:

φ = φ0 - dt div(J(η))
η = (ψ'(φ) + δψ'(φ, φ0)) σ / ε - σ ε Δ(φ)

For stability we wish for the perturbation δψ to be such that the time discrete system preserves the energy dissipation property E(φ) ≤ E(φ0) for any timestep dt. To derive suitable perturbation terms to this effect, we define without loss of generality δψ'(φ, φ0) = .5 (φ - φ0) f(φ, φ0) and derive the following condition for unconditional stability:

E(φ) - E(φ0) = ∫_Ω .5 (1 - φ² - .5 (φ + φ0)² - f(φ, φ0)) (φ - φ0)² σ / ε
             - ∫_Ω (.5 σ ε ‖∇φ - ∇φ0‖² + dt M ‖∇η‖²) ≤ 0

The inequality holds true if the perturbation f is bounded from below such that f(φ, φ0) ≥ 1 - φ² - .5 (φ + φ0)². To keep the energy minima at the pure phases we additionally impose that f(±1, φ0) = 0, and select 1 - φ² as a suitable upper bound which we will call "nonlinear".

We next observe that η is linear in φ if f(φ, φ0) = g(φ0) - φ² - (φ + φ0)² for any function g, which dominates if g(φ0) ≥ 1 + .5 (φ + φ0)². While this cannot be made to hold true for all φ, we make it hold for -√2 ≤ φ, φ0 ≤ √2 by defining g(φ0) = 2 + 2 |φ0| + φ0², which we will call "linear". This scheme further satisfies a weak minima preservation f(±1, ±|φ0|) = 0.

We have thus arrived at the three stabilization schemes implemented here:

• nonlinear: f(φ, φ0) = 1 - φ²
• linear: f(φ, φ0) = 2 + 2 |φ0| - 2 φ (φ + φ0)
• none: f(φ, φ0) = 0 (not unconditionally stable)

Finally, we observe that the weak formulation:

∀ δη: ∫_Ω [ dt J(η)·∇δη - δη (φ - φ0) ] = 0
∀ δφ: ∫_Ω [ δφ (ψ'(φ) + δψ'(φ, φ0)) σ / ε + σ ε ∇(δφ)·∇(φ) ] = ∫_Γ -δφ σd

is equivalent to the optimization problem ∂F/∂φ = ∂F/∂η = 0, where

F(φ, φ0, η) := E(φ) + ∫_Ω [ .5 dt J(η)·∇η + δψ(φ, φ0) σ / ε - η (φ - φ0) ]

For this reason, the stab enum in this script defines the stabilizing term δψ, rather than f, allowing Nutils to construct the residuals through automatic differentiation using the optimize method.