By Evalf, and other Nutils contributors

officialhierarchical refinementsLaplace

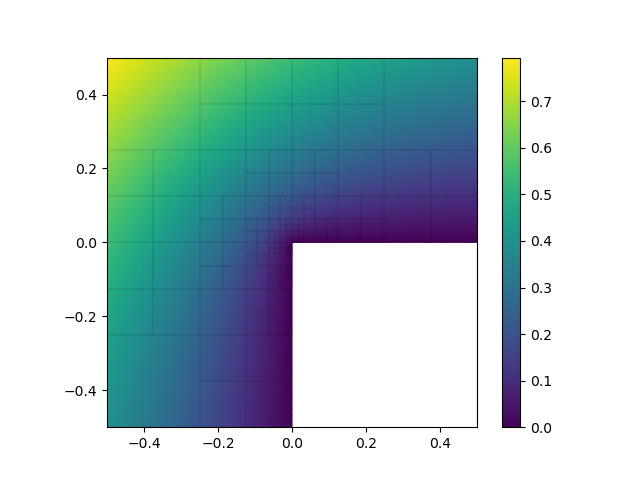
Solves the Laplace problem on a unit square that has the bottom-right quadrant removed (a.k.a. an L-shaped domain) with Dirichlet boundary conditions matching the harmonic function

³√(x² + y²) cos(⅔ arctan2(y+x, y-x))

shifted by ½ such that the origin coincides with the center of the unit square. Note that the function evaluates to zero where the domain borders the removed quadrant.

This benchmark problem is known to converge suboptimally under uniform refinement due to a singular gradient in the reentrant corner. This script demonstrates that optimal convergence rates of -(p+1)/2 for the L2 norm and -p/2 for the H1 norm can be restored by using adaptive refinement.